Présentation de notre simulateur RESCU-DFPT par une approche innovante afin de prédire les propriétés des matériaux : constante diélectrique statique

Le développement de RESCU a commencé il y a plus de cinq ans dans le but de continuer les travaux de Zhou et al. [1, 2]. Au sein de notre compagnie Nanoacademic Technologies Inc., ici à Montréal, il est devenu un outil KS-DFT (Kohn-Sham) puissant qui résout l’équation KS sur des grilles spatiales réelles en utilisant la méthode des filtres de Chebyshev (en abrégé CFSI, acronyme que nous garderons dans cet article). Cette méthode CFSI évolue favorablement avec le nombre d’atomes et permet à RESCU de simuler efficacement de grands systèmes qui sont hors de portée des solveurs conventionnels. La suite RESCU comprend également un module avec plusieurs fonctionnalités qui sont en constante évolution pour simuler les réponses des matériaux basées sur une implémentation dans l’espace réel de la théorie des perturbations fonctionnelles de la densité (notée DFPT). L’ensemble des fonctionnalités actuelles de notre module propriétaire DFPT comprend les quantités physiques suivantes, rassemblées dans la Figure 1 ci-dessous:

Figure 1 – Liste des fonctionnalités du module DFPT de notre solveur RESCU

Afin d’étendre les applications DFPT à des systèmes plus grands tout en mettant le module sur un pied d’égalité avec les simulations à l’état fondamental en ce qui concerne la taille du système, nous avons franchi une étape cruciale et avons porté la méthode CFSI au sein de la DFPT, ce qui a donné naissance à la méthode des filtres de Chebyshev perturbés (notée par la suite PCFSI) [3]. Dans ce bref article, nous montrerons comment la PCFSI est utilisée pour calculer un paramètre classique : la constante diélectrique des matériaux.

La constante diélectrique statique est la réponse linéaire à un champ électrique homogène statique externe. Bien qu’elle puisse être calculée par différence finie, la DFPT est la méthode de pointe pour traiter les systèmes perturbés car elle offre de nombreux avantages de calcul par rapport aux méthodes directes. Elle ne nécessite pas de simulation de supercellules (qui sont coûteuses en temps de calcul) et elle est relativement exempte de paramètres (ce qui facilite l’évaluation de la précision des résultats). Dans le tableau ci-dessous, la précision de notre nouvelle méthode PCFSI est démontrée par comparaison avec les résultats d’autres simulations numériques disponibles et contre les données expérimentales :

Figure 2 – Nos résultats étalons par rapport à un autre code et aux données expérimentales, établissant une référence.

Le solveur basé sur la méthode PCFSI renvoie les mêmes résultats que les codes conventionnels basés sur des algorithmes avancés tels que la technique du gradient conjugué préconditionné (PCG). Cependant, il s’adapte mieux au nombre d’atomes et est donc plus efficace pour les problèmes à grande échelle. Notons qu’il est plus facile à paralléliser et a une empreinte mémoire moindre comme dans le cas des calculs à l’état fondamental. Il surpasse ainsi généralement le PCG sur les processeurs modernes qui sont multicœurs et les clusters. Nous avons testé cela en calculant la constante diélectrique pour des supercellules de nitrure de bore (BN) de tailles croissantes :

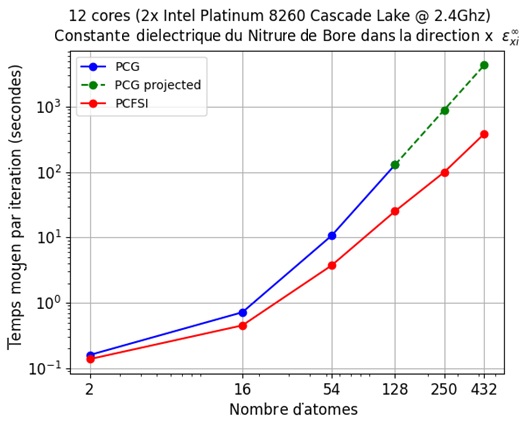
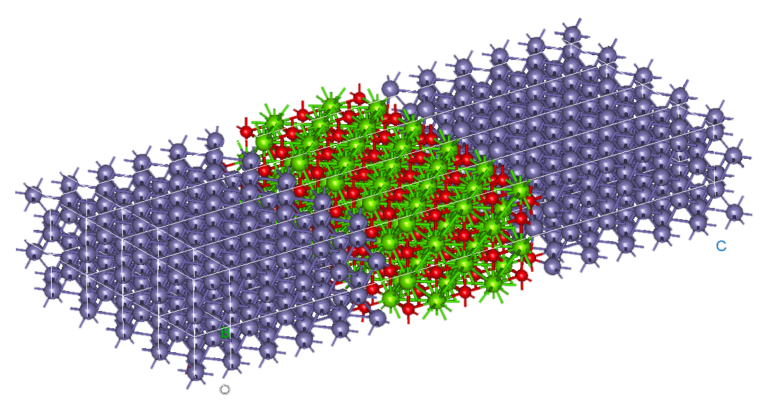
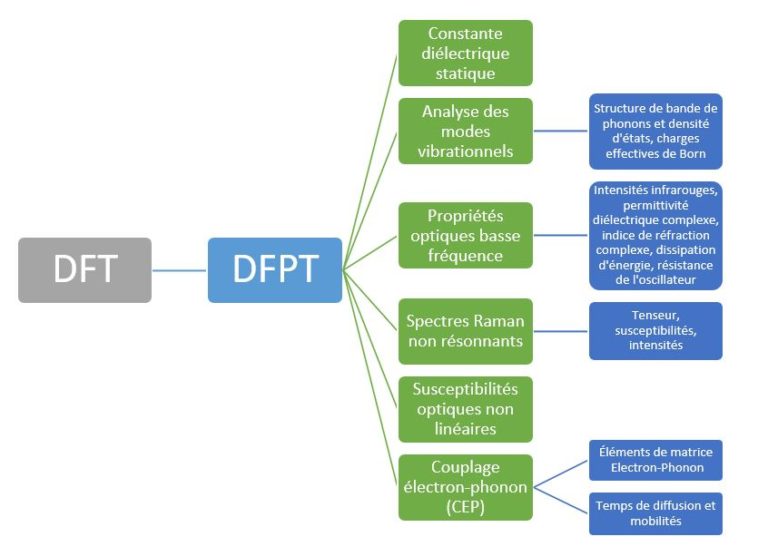
Figure 3 – Les gains de temps de calcul obtenus par notre méthode PCFSI vs taille des supercellules qui augmente.

Ce résultat obtenu pour le BN peut être généralisé à d’autres types de matériaux : avec l’augmentation de la taille des cellules, notre méthode devient prédominante par rapport à toute autre méthode comparable.

Nous voyons que la méthode PCFSI surpasse déjà le PCG en utilisant 12 cœurs pour une cellule de taille unitaire et l’écart se creuse rapidement à mesure que la taille du système augmente, de sorte qu’il est environ 8 fois plus rapide pour les supercellules à 128 atomes. Parce que la PCFSI a des besoins inférieurs en mémoire, elle peut être utilisée pour simuler des supercellules jusqu’à 432 atomes tandis que le solveur PGC ne pouvait simuler que des systèmes avec 128 atomes maximum dans le test d’étalonnage ci-dessus. Plus de détails sur l’algorithme PCFSI (matrice dynamique, structure de bande et densité d’états phononiques, spectre Raman, etc.) seront donnés dans nos prochaines publications ici sur LinkedIn : alors pour ne pas les manquer, nous vous invitons à nous suivre pour être informés de notre actualité. Nous montrerons que celui-ci peut être adapté pour calculer toutes les réponses fonctionnelles typiquement obtenues par DFPT.

Nous espérons que vous avez apprécié la lecture de cet article, merci et n’hésitez pas à commenter et à nous demander des informations spécifiques sur nos outils atomistiques et méthodes mises en œuvre, nous serons plus qu’heureux de vous donner des informations supplémentaires et vous faire tester nos outils.

Plus de contenu sur la science de la simulation à venir très bientôt !

[1] Zhou, Y., Saad, Y., Tiago, M., & Chelikowsky, J. (2006). Parallel self-consistent-field calculations via Chebyshev-filtered subspace acceleration. Physical Review E, 74(6), 066704. https://doi.org/10.1103/PhysRevE.74.066704

[2] Michaud-Rioux, V., & Guo, H. (2017). RESCU: extending the realm of Kohn-Sham density functional theory. https://escholarship.mcgill.ca/concern/theses/dn39x387d?locale=en

[3] Bohloul, S. (2017). First-Principles Quantum Transport and Linear Response Modeling of Nano-devices and Materials. https://escholarship.mcgill.ca/concern/theses/8910jx167?locale=en

[4] Gajdoš, M., Hummer, K., Kresse, G., Furthmüller, J., & Bechstedt, F. (2006). Linear optical properties in the projector-augmented wave methodology. Physical Review B – Condensed Matter and Materials Physics, 73(4), 045112. https://doi.org/10.1103/PhysRevB.73.045112

[5] A. Jain*, S.P. Ong*, G. Hautier, W. Chen, W.D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder, K.A. Persson (*=equal contributions), The Materials Project: A materials genome approach to accelerating materials innovation, APL Materials, 2013, 1(1), 011002.