Présentation d’une autre fonctionnalité de notre méthode de simulation RESCU-DFPT : modélisation des charges effectives de Born et division LO-TO

Dans les articles précédents, nous avons démontré comment le module Density Functional Perturbation Theory (DFPT) de notre outil atomistique RESCU peut être utilisé pour calculer la constante diélectrique ionique (ou statique), la structure de bandes de phonons et la densité d’états des matériaux avec une bande interdite. Dans cet article, nous montrons comment le module DFPT de notre solveur permet de calculer les charges effectives de Born (BEC) dans les matériaux isolants ou semiconducteurs et de prédire la correction de la division LO-TO pour les énergies des phonons.

Figure 1 – Liste de nos principales fonctionnalités DFPT au sein de notre solveur RESCU.

Les BEC quantifient le couplage entre les phonons optiques en limite de grande longueur d’onde et les champs électriques, autrement dit c’est le coefficient de proportionnalité entre la réponse de polarisation dans une direction provoquée par un déplacement atomique dans une autre direction [1]. Les BEC modifient certaines propriétés des matériaux et il est essentiel d’inclure leur effet dans les simulations atomistiques. À titre d’exemple, calculons les BEC de quelques systemes bimoléculaires tels que AlAs et de BN, les valeurs correspondantes sont répertoriées dans le tableau ci-dessous :

Table 1 – Calculs des BEC pour 2 systèmes simples

Un système neutre doit également être neutre en BEC, car les BEC ne tiennent pas compte de la charge macroscopique. Cela peut être vu dans le tableau ci-dessus où le BEC net pour chaque système est égal à zéro (les petits écarts par rapport à zéro sont dus à des inexactitudes numériques). Cependant, les BEC induisent un champ électrique interne à l’intérieur du matériau entre les centres atomiques positifs et négatifs. Ce champ exerce une force supplémentaire sur les atomes qui à son tour affecte leurs propriétés vibrationnelles (phonons). L’effet de cette force est clairement visible dans la structure de la bande de phonons.

Nous calculons la structure de bande de phonons d’AlAs et de BN à l’aide de notre module DFPT à l’aide de fonctionnelles d’échange-corrélation PBE (comme démontré dans nos articles précédents). Cela est illustrées dans les figures (2) et (3) ci-dessous :

Figure 2 – Structure de bandes phononique du Nitrure de Bore calculée avec notre méthode DFPT

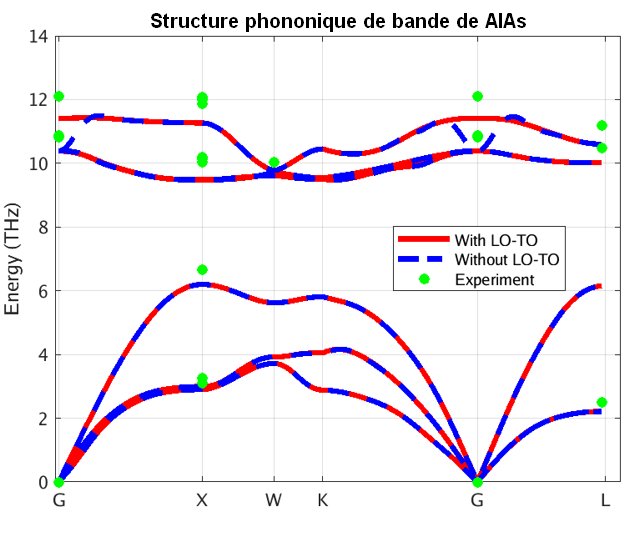
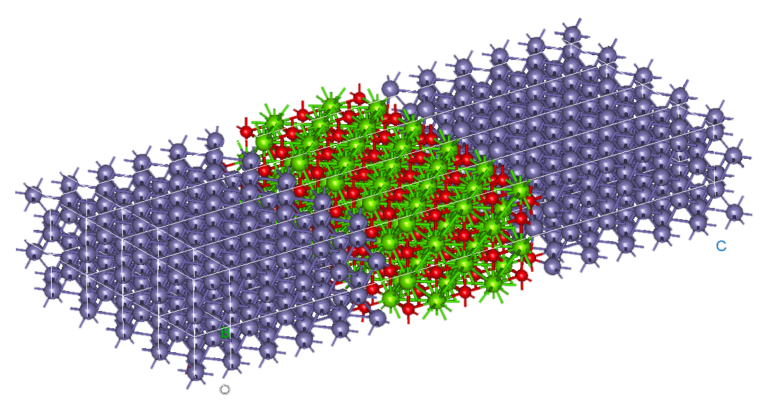
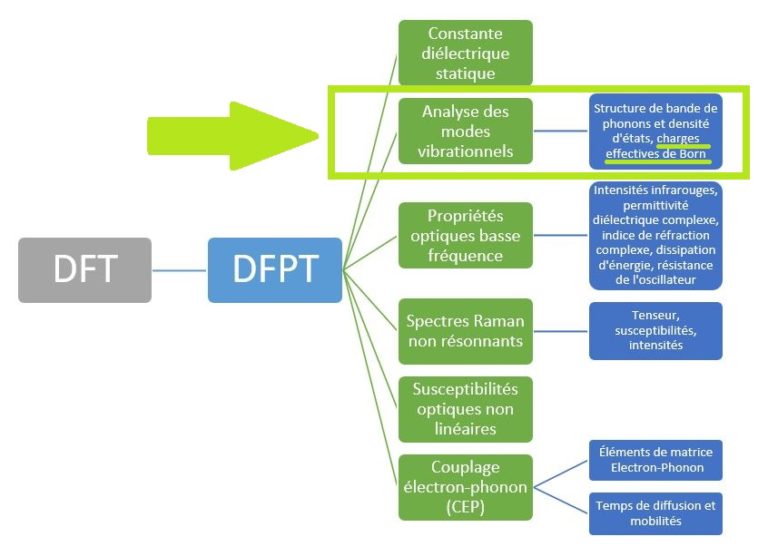
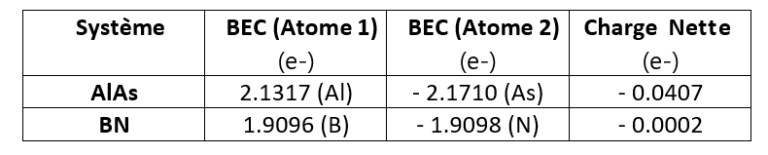
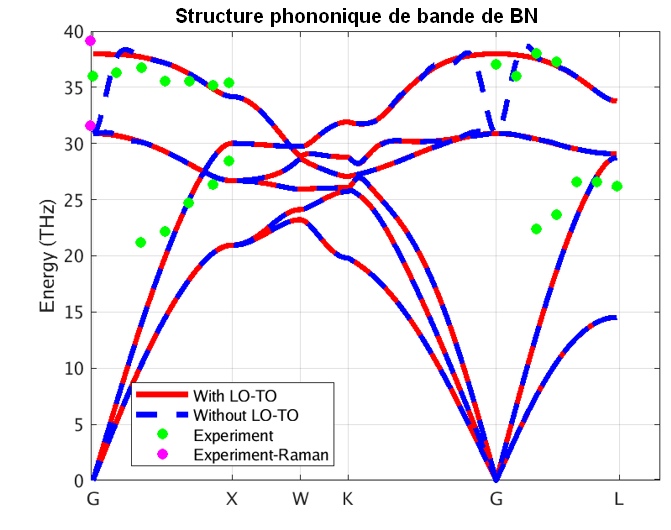
Figure 3 – Structure de bandes phononique de l’Arseniure d’Aluminium calculée avec notre méthode DFPT

Sur ces figures, les lignes bleues et rouges représentent les énergies de phonons calculées respectivement sans et avec effet des BEC. La division des énergies des phonons pour les modes optiques transversaux et longitudinaux (TO et LO) est aussi clairement visible en comparant les structures des bandes bleue et rouge. Le dédoublement LO-TO peut également être observé dans les données expérimentales (illustrées en vert et violet) où l’effet lève la dégénérescence des modes LO et TO (BN [2] et AlAs [3]). Comme indiqué ci-dessus, cela est dû au champ électrique induit des BEC qui exercent une force supplémentaire sur les atomes en mode LO. Les énergies des modes LO dans AlAs et BN sont augmentées d’environ 1 et 7 THz respectivement, ce qui constitue une correction significative.

Notre simulation PBE capture les informations essentielles concernant les spectres de phonons pour ces systèmes, y compris la division LO-TO. Il s’avère que le spectre de phonons de la LDA (Local Density Approximation) d’AlAs et de BN (non illustré ici) se compare mieux aux données expérimentales rapportées. Notons cependant que les mesures expérimentales sont rares et dispersées autour des prédictions théoriques. De plus, les simulations théoriques prédisent correctement le comportement linéaire des phonons acoustiques (raies Γ-X et Γ-L proches de Γ), contrairement aux mesures expérimentales. Ceci témoigne de la difficulté de mesurer les spectres de phonons et motive le besoin d’un codes de principes premiers comme RESCU qui soit précis et efficaces pour parvenir à cela.

Dans une publication à venir ici sur LinkedIn, nous montrerons comment le module DFPT utilise les ingrédients susmentionnés pour calculer les propriétés optiques telles que les intensités infrarouges, la permittivité diélectrique dépendante de la fréquence et l’indice de réfraction.

Nous espérons que vous avez apprécié cette brève lecture, merci et n’hésitez pas à commenter et à nous demander des informations spécifiques sur nos outils atomistiques, nous serons plus qu’heureux de vous donner des informations supplémentaires comme à l’accoutumée.

Plus de contenu sur la science de la simulation est définitivement au coin de la rue, avec des nouvelles prochainement sur nos prochains outils et fonctionnalités, alors suivez-nous et connectons-nous pour ne rien manquer des prochains articles !

[1] Xavier Gonze and Changyol Lee (1997). Dynamical matrices, Born effective charges, dielectric permittivity tensors, and interatomic force constants from density-functional perturbation theory: Phys. Rev. B 55, 10355 – Published 15 April 1997

[2] Hage, F. S., Nicholls, R. J., Yates, J. R., McCulloch, D. G., Lovejoy, T. C., Dellby, N., Krivanek, O. L., Refson, K., & Ramasse, Q. M. (2018). Nanoscale momentum-resolved vibrational spectroscopy. Science Advances, 4(6), eaar7495. https://doi.org/10.1126/SCIADV.AAR7495

[3] Azuhata, T., Sota, T., & Suzuki, K. (1995). Second-order Raman spectra and lattice dynamics in AlAs. Journal of Physics: Condensed Matter, 7(9), 1949. https://doi.org/10.1088/0953-8984/7/9/018