Introducing the RESCU-DFPT simulator: an innovative approach to predicting material properties: ion-clamped dielectric constant

RESCU began more than five years ago with the goal of extending the work of Zhou et al. [1, 2]. At Nanoacademic Technologies Inc., it grew into a powerful KS-DFT solver (Kohn-Sham), which solves the KS equation on real space grids by using the Chebyshev filtered subspace iteration (abbreviated CFSI) method. CFSI scales efficiently with the number of atoms and empowers RESCU to simulate large systems which are beyond the reach of conventional solvers.

The RESCU suite also includes a feature-rich and ever-growing module for simulating materials response functions based on real-space implementation of density functional perturbation theory (DFPT). The current feature stack of our DFPT module includes the following physical quantities:

Figure 1 – List of our core RESCU DFPT features.

To extend DFPT applications to larger systems and put RESCU ground-state and response function simulations on equal footings with respect to system size, we took a crucial step and ported the CFSI method to the DFPT framework which gave birth to perturbed Chebyshev filter subspace iteration (PCFSI) algorithm [3]. In this brief article, we shall show how PCFSI is used to calculate a classical parameter: the dielectric constant of materials.

The (ion-clamped) dielectric constant is the linear response to an external static homogeneous electric field. Although it can be calculated by finite difference, DFPT is the state-of-the-art method to deal with perturbed systems as it offers many computational advantages over direct methods. It does not require simulating supercells (which are computationally expensive) and it is relatively parameter free (which makes assessing the accuracy of results easier). In the table below, the accuracy of our novel PCFSI method is demonstrated by comparison with results from other numerical simulations and experimental data. See Figure 2:

Figure 2 – Our results versus another market code versus experiments: comparison is set.

The PCFSI-based solver returns the same results as conventional solvers for linear systems, such as the state-of-the-art preconditioned conjugate gradient (PCG) algorithm. However, it scales better with respect to the number of atoms, and hence it is generally more efficient for large scale problems. We note that is it more parallelizable and has a lesser memory footprint as in the case of ground state calculations. It thus generally outperforms PCG on modern multicore processors and clusters. We tested this by computing the dielectric constant for supercells of boron nitride (BN) of increasing sizes (Figure 3):

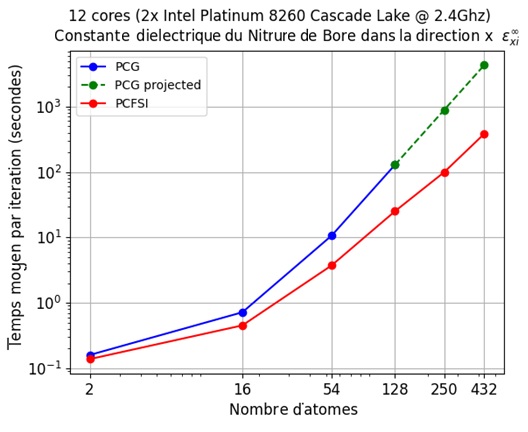
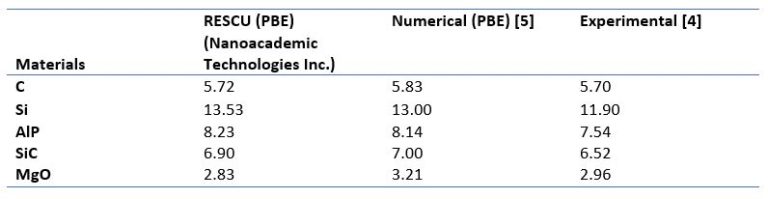
Figure 3 – The computational time gains of our PCFSI method while supercell sizes increase.

This result obtained for BN can be generalized to other types of materials: with increasing cell sizes our method becomes prevalent Vs any other methods in those case studies.

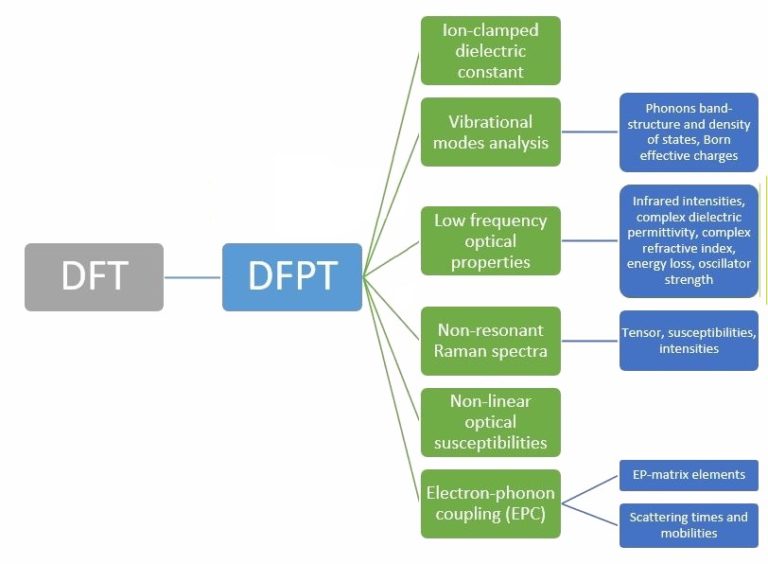
We see that PCFSI already outperforms PCG using 12 cores for all unit cell sizes and the gap is growing rapidly as system size increases, such that it is around 8 times faster for supercell with 128 atoms. Because PCFSI has lower memory requirements, it can be used to simulate supercells up to 432 atoms while the PGC solver could only simulate systems with 128 atoms in the above benchmark. More details on the PCFSI algorithm (dynamical matrix, phonon band-structure and density of states, Raman spectrum, and more) will be explained in forthcoming publications here on LinkedIn, so do not miss them! We will show it can be adapted to compute all response functions typically obtained in DFPT.

We hope you enjoyed the read, thank you and feel free to comment and ask us specific information about our atomistic tools, we will be more than happy to give additional insights.

More simulation science content to come very soon! Please stay tuned.

[1] Zhou, Y., Saad, Y., Tiago, M., & Chelikowsky, J. (2006). Parallel self-consistent-field calculations via Chebyshev-filtered subspace acceleration. Physical Review E, 74(6), 066704. https://doi.org/10.1103/PhysRevE.74.066704

[2] Michaud-Rioux, V., & Guo, H. (2017). RESCU: extending the realm of Kohn-Sham density functional theory. https://escholarship.mcgill.ca/concern/theses/dn39x387d?locale=en

[3] Bohloul, S. (2017). First-Principles Quantum Transport and Linear Response Modeling of Nano-devices and Materials. https://escholarship.mcgill.ca/concern/theses/8910jx167?locale=en

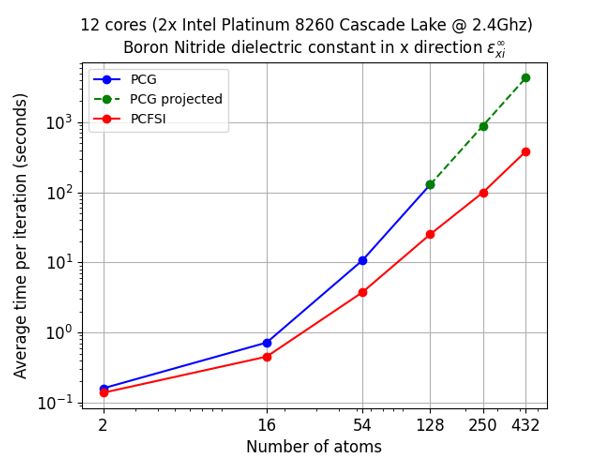
[4] Gajdoš, M., Hummer, K., Kresse, G., Furthmüller, J., & Bechstedt, F. (2006). Linear optical properties in the projector-augmented wave methodology. Physical Review B – Condensed Matter and Materials Physics, 73(4), 045112. https://doi.org/10.1103/PhysRevB.73.045112

[5] A. Jain*, S.P. Ong*, G. Hautier, W. Chen, W.D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder, K.A. Persson (*=equal contributions), The Materials Project: A materials genome approach to accelerating materials innovation, APL Materials, 2013, 1(1), 011002.