In previous posts, we demonstrated how the Density Functional Perturbation Theory (DFPT) module of our atomistic tool RESCU can be used to compute the ion-clamped dielectric constant, phonons band structure and density of states of materials with an electronic bandgap (semiconductors and insulators).
In this article we show how the DFPT module of our advanced solver RESCU enables computing the Born effective charges (BECs) in polar gapped materials and predicting the so-called LO-TO splitting correction to phonon energies.
Figure 1 – List of our core RESCU DFPT features.
BECs quantify the coupling between the optical phonons in long wavelength limit and electric fields, in other words it is the coefficient of proportionality between the polarization response in one direction caused by an atomic displacement in another direction [1]. The BECs modify certain material properties and it is essential to include their effect in atomistic simulations. As an example, let’s compute BECs of AlAs and BN, the corresponding values are listed in the table below:
Table 1 – BEC calculation for 2 reference systems: BN and AlAs
A neutral system should also be BEC-neutral, since BECs do not account for macroscopic charge. This can be seen from the table above where the net BEC for each system sums to zero (small deviations from zero are due to numerical inaccuracies). However, BECs induce an internal electric field inside the material between the positive and negative atomic centers. This field exerts an extra force upon atoms which in turn affects their vibrational properties (phonons). The effect of this force is clearly visible in the phonon band structure.
We compute the phonon band structure of AlAs and BN using our DFPT module using PBE exchange-correlation functionals (as demonstrated in our previous posts), illustrated in Figures (2) and (3) below:
Figure 2 – Phonon band structure of BN using our DFPT module
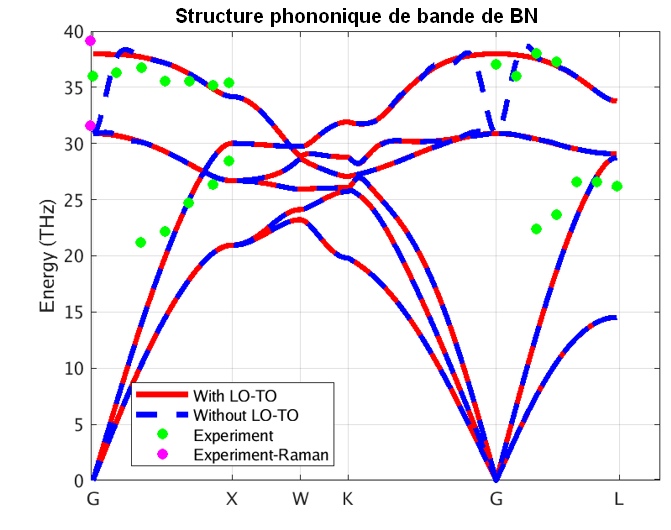
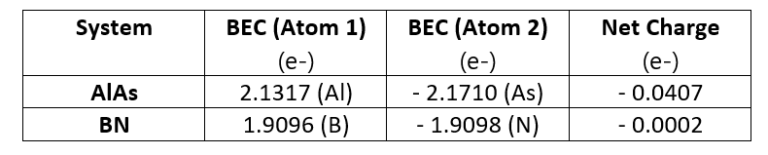
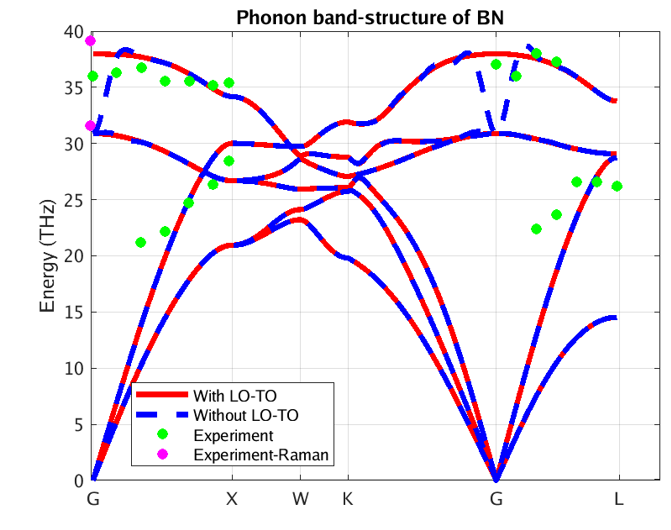
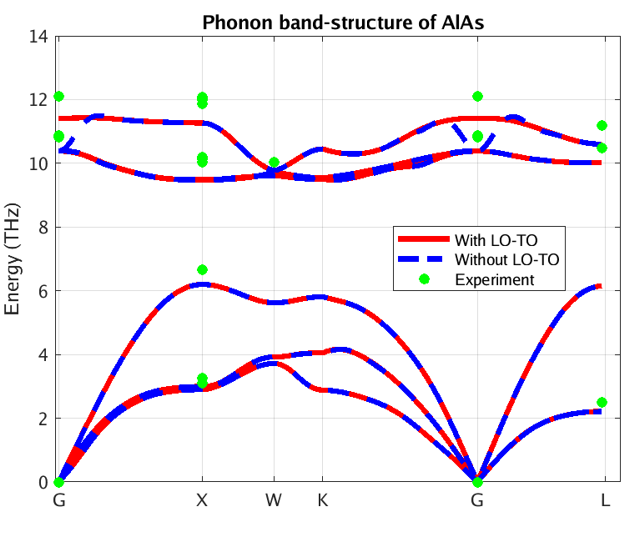
Figure 3 – Phonon band structure of AlAs using our DFPT module
In these figures, the blue and red lines represent computed phonon energies without and with BECs effect respectively. The splitting of phonon energies for transverse and longitudinal optical phonons (TO and LO) modes at Γ is clearly seen by comparing the blue and red band structures. LO-TO splitting can also be observed in the experimental data (illustrated in green and purple) at Γ, where the effect lifts the degeneracy of LO and TO modes (BN [2] and AlAs [3]). As stated above, this is due to the induced electric field of BECS which exerts extra force on atoms in LO mode. The energies of the LO modes in AlAs and BN are increased by roughly 1 and 7 THz respectively, a significant correction.
Our PBE simulation captures the essential information regarding phonon spectra for these systems, including the LO-TO splitting. As it turns out, the LDA (Local Density Approximation) phonon spectrum of AlAs and BN (not shown here) compares better with the reported experimental data. Note, however, that experimental measurements are scarce and scattered around theoretical predictions. Moreover, theoretical simulations correctly predict the linear behavior of acoustic phonons (Γ-X and Γ-L lines close to Γ), whereas experimental measurements do not. This testifies to the difficulty of measuring phonon spectra and motivates the need for accurate and efficient first principles codes.
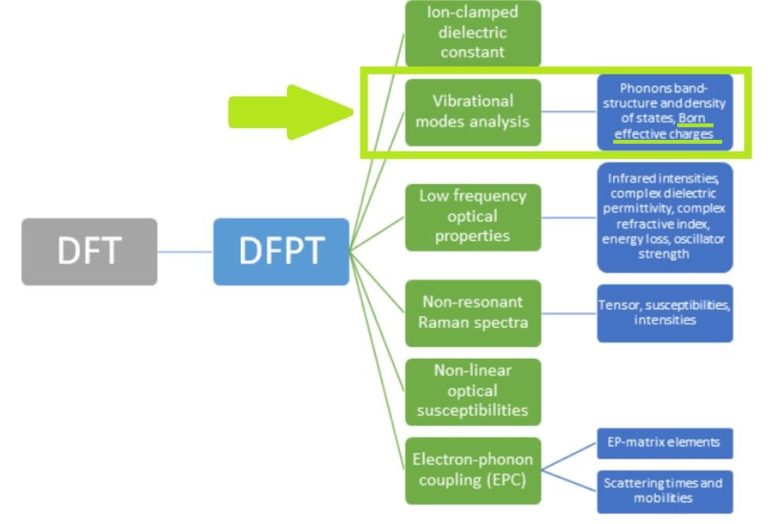
In a forthcoming publication here on LinkedIn, we will show how the DFPT module uses the aforementioned ingredients to compute optical properties like infrared intensities, frequency dependent dielectric permittivity and the index of refraction.
We hope you enjoyed the read, thank you and feel free to comment and ask us specific information about our atomistic tools, we will be more than happy to give additional insights.
After this well-deserved summer-break, more simulation science content is definitely around the corner so please follow us and connect with us not to miss any of the next posts!
———————–
[1] Xavier Gonze and Changyol Lee (1997). Dynamical matrices, Born effective charges, dielectric permittivity tensors, and interatomic force constants from density-functional perturbation theory: Phys. Rev. B 55, 10355 – Published 15 April 1997
[2] Hage, F. S., Nicholls, R. J., Yates, J. R., McCulloch, D. G., Lovejoy, T. C., Dellby, N., Krivanek, O. L., Refson, K., & Ramasse, Q. M. (2018). Nanoscale momentum-resolved vibrational spectroscopy. Science Advances, 4(6), eaar7495. https://doi.org/10.1126/SCIADV.AAR7495
[3] Azuhata, T., Sota, T., & Suzuki, K. (1995). Second-order Raman spectra and lattice dynamics in AlAs. Journal of Physics: Condensed Matter, 7(9), 1949. https://doi.org/10.1088/0953-8984/7/9/018
