Introduction d’une autre fonctionnalité de notre outil RESCU utilisant la DFPT : représentations de structures phononiques de cristaux élémentaires

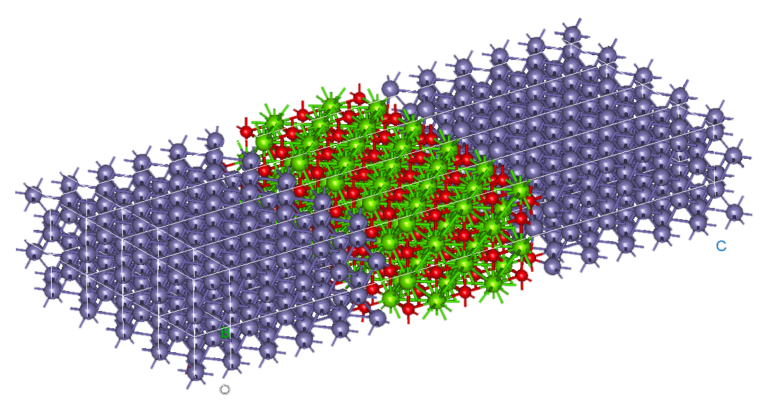
Notre outil atomistique RESCU est un puissant solveur KS-DFT (Kohn-Sham) qui résout l’équation KS sur des grilles spatiales réelles en utilisant la méthode d’itération sous-spatiale filtrée de Chebyshev (CFSI). Cette méthode CFSI évolue favorablementt avec le nombre d’atomes et les ressources de calcul disponibles, ce qui permet à RESCU de simuler de grands systèmes qui sont hors de portée des solveurs conventionnels.

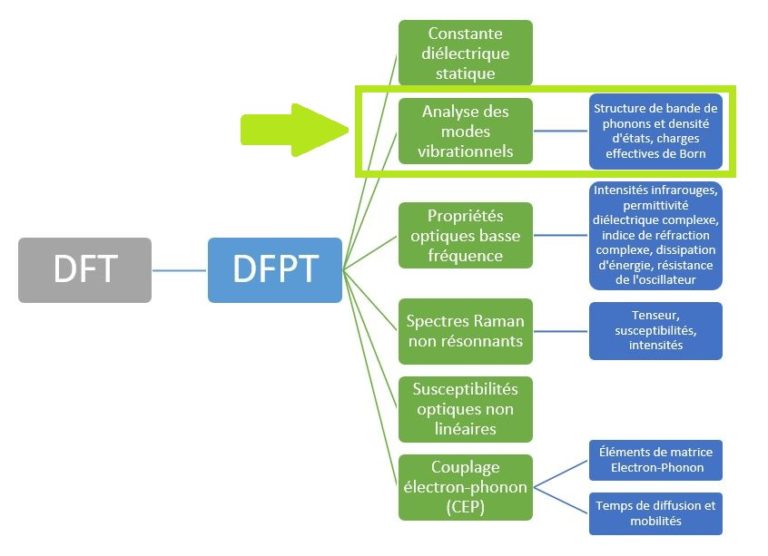
Dans notre précédent article posté fin Juin, nous avions présenté notre boîte à outils de la théorie de la fonctionnelle de la densité perturbée (DFPT) et avions aussi introduit la méthode dite CFSI perturbée (PCFSI) comme notre solution unique pour les simulations DFPT à grande échelle. Nous avons démontré comment cela permet de calculer la constante diélectrique ionique (ou statique) aussi précisément que les techniques DFPT de pointe, tout en étant plus efficace et en nous permettant de simuler des systèmes jusqu’à plusieurs centaines d’atomes. Pour rappel ou pour ceux qui ont raté nos publications précédentes, l’ensemble actuel des fonctionnalités de la boîte à outils DFPT est résumé dans le schéma suivant (Figure 1) :

Figure 1 – Liste de nos principales fonctionnalités DFPT au sein de notre solveur RESCU.

Dans cet article, nous nous concentrons sur les déplacements atomiques en tant que facteurs de perturbation et démontrons comment la DFPT avec l’algorithme PCFSI peut être utilisée pour calculer avec précision les spectres de phonons de matériaux comprenant des centaines d’atomes. Commençons par démontrer la précision du formalisme DFPT en comparant la structure de bandes de phonons de deux des semi-conducteurs élémentaires parmi les plus importants : le diamant et le silicium.

La figure (1) illustre la structure de bandes de phonons simulée du diamant (en utilisant la fonction d’échange-corrélation GGA) par rapport aux données expérimentales (cercles bleus). Nous pouvons voir comment les résultats de la simulation suivent de près les points de données expérimentaux :

Figure 2 – Structure de bandes de phonons du diamant cubique à faces centrées (CFC) : des résultats d’expériences par rapport à notre simulation montrant une correspondance très étroite.

Nous observons également la même précision en comparant la structure de bande de phonons simulée du silicium (dans la phase de réseau de diamant et en utilisant la fonction d’échange-corrélation GGA) avec des données expérimentales (cercles bleus) :

Figure 3 – Structure de bandes de phonons du silicium cubique à faces centrées (CFC) : des résultats expérimentaux Vs notre simulation, qui sont également très proches !

Les données expérimentales ont été extraites de [1, 3] à l’aide d’un numériseur de tracé [2]. Dans l’ensemble, nous voyons que la DFPT fournit des prédictions quantitatives du spectre de phonons de divers matériaux. Dans le cas présent, on note une légère sous-estimation des énergies des phonons optiques les plus énergétiques (de l’ordre de 20 cm-1).

Ensuite, nous démontrons l’efficacité de la méthode PCFSI dans le traitement de systèmes plus lourds, en calculant la densité d’états de phonons (DOS) d’une supercellule de diamant comprenant 216 atomes. Comme il est très coûteux en calcul (voire impossible en raison des besoins en mémoire et du temps de calcul long) de générer les mêmes résultats avec une méthode conventionnelle de comparaison, nous adoptons une approche différente pour montrer la précision de notre simulation. Nous simulons un diamant à 8 atomes (cellule unitaire conventionnelle) avec un échantillonnage q élevé via un solveur conventionnel et 64 (soit 8 fois plus) et 216 (soit 27 fois plus) supercellules avec la méthode PCFSI. Nous voyons facilement que la DOS de la supercellule à 216 atomes se trouve juste au-dessus de la DOS de la cellule conventionnelle à échantillonnage élevé. En d’autres termes, nous obtenons les mêmes résultats pour des simulations avec des paramètres de calcul convergents (ici, avec échantillonnage q élevé pour la cellule conventionnelle et grande maille unitaire pour la supercellule) représentant la même réalité physique. En revanche, la DOS de la supercellule à 64 atomes présente des différences mineures car il n’est pas assez grand pour résoudre toutes les forces interatomiques à longue distance si seulement gamma-échantillonné :

Figure 4 – Densité d’états des phonons du diamant : 216 atomes sont nécessaires pour retrouver la limite d’échantillonnage q élevée (d’une maille unitaire conventionnelle).

En termes d’efficacité, la supercellule de 64 atomes aurait été un défi sur un seul nœud et un système de 216 atomes fut été impossible en raison des besoins en mémoire, mais cela n’a posé aucun problème à notre propre implémentation PCFSI. Alors qu’il ne faut qu’environ 30 minutes pour simuler un déplacement atomique avec PCFSI sur un petit nombre de CPU (48), il faudrait une durée d’un ordre de grandeur supplémentaire (5 heures ou plus) pour effectuer la même simulation avec un solveur conventionnel. En général, pour un système composé de N atomes, nous devons effectuer 3xN de telles opérations de calculs pour chaque point q (vecteur d’onde de phonons) pour obtenir le spectre complet phononique, ce qui souligne l’importance de la performance du solveur utilisant PCFSI pour les calculs de supercellules. Le tableau suivant répertorie certains temps de calculs concernant nos simulations sur les systèmes diamants :

Tableau 1 – Temps de calcul pour les supercellules de diamant.

Dans cet article, nous avons montré que notre outil atomistique RESCU peut calculer avec précision les spectres phononiques de matériaux comprenant des centaines d’atomes. La structure de bandes de phonons dans les matériaux polaires est affectée par le couplage du champ électrique avec les vibrations longitudinales qui est réalisé par l’introduction de charges effectives de Born : dans une publication à venir prochainement ici sur LinkedIn, nous expliquerons comment calculer ces charges effectives de Born et corriger la structure de bandes de phonons des matériaux polaires qui conduit à ce qu’on appelle la scission LO-TO.

Nous espérons que vous avez apprécié la lecture, merci et n’hésitez pas à commenter ou nous écrire en messages directs comme d’habitude pour nous demander des informations spécifiques sur nos outils atomistiques, nous serons plus qu’heureux de vous donner des informations supplémentaires.

Plus de contenu sur la Science de la simulation à venir très bientôt !

[1] Gonze, X., Rignanese, G., & Caracas, R. (2005). First-principle studies of the lattice dynamics of crystals, and related properties. Zeitschrift für Kristallographie – Crystalline Materials, 220, 458 – 472.

[2] https://apps.automeris.io/wpd/

[3] Kulda, Strauch, Pavone, & Ishii (1994). Inelastic-neutron-scattering study of phonon eigenvectors and frequencies in Si. Physical review. B, Condensed matter, 50 18, 13347-13354.