Article rédigé par: Dr. Mohammed Harb, Dr. Wanting Zhang, Dr. Vincent Michaud-Rioux et M. Jeremy F. Garaffa.
L’une des étapes les plus difficiles du processus de simulation d’un matériau consiste à adopter une description de son noyau et de ses électrons qui soit à la fois :
- – Précision
- – Performance computationnelle
Dans cet article de blog, également disponible sur notre page LinkedIn, nous présenterons un aperçu rapide de quelques descriptions couramment utilisées pour les électrons de noyau, de noyau et de valence et présenterons nos propres orbitales atomiques numériques (NAO) nouvellement optimisées pour la fonctionnelle Perdew-Burke-Ernzerhof (PBE).
Nucléons et électrons de cœur:
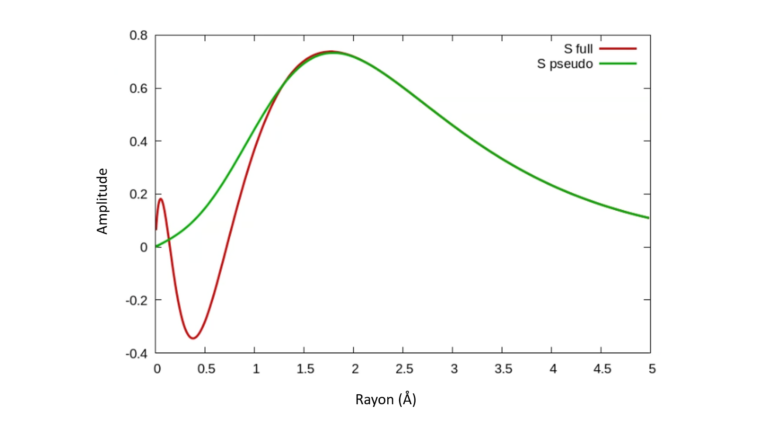
Les électrons de cœur sont généralement inertes vis-à-vis de l’environnement chimique en raison de leurs grandes énergies de liaison. Il est donc possible de simplifier leur description en remplaçant le potentiel nu de tous les électrons par un « pseudo potentiel » plus simple – un terme qui capture l’effet net des électrons du noyau et du noyau sans qu’il soit nécessaire de considérer le potentiel de Coulomb singulier. La méthode permet également de supprimer les caractéristiques nettes des fonctions d’onde de valence près de l’origine. A titre d’exemple, la figure 1 montre la pseudo-fonction d’onde de Si obtenue à partir d’un pseudo potentiel et la compare à la fonction d’onde résultant du potentiel nu. La pseudo-fonction d’onde se comporte mieux et a moins de nœuds et reproduit pourtant une densité de charge identique à la vraie fonction d’onde au-delà d’un rayon critique (~ 1 Å soit 0.1 nanomètre).