v1.0 of our Atomic Orbital database is released!

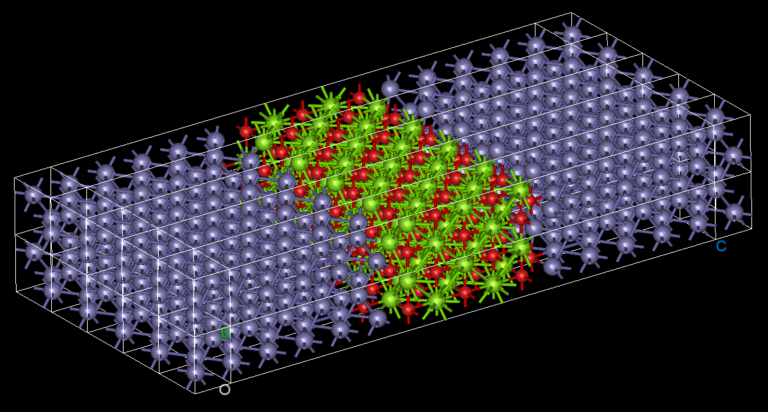
By Dr. Mohammed Harb, Dr. Wanting Zhang, Dr. Vincent Michaud-Rioux and Mr. Jeremy F. Garaffa.

One of the most challenging steps in the process of simulating a material is adopting a description of its nucleus and electrons which is both:

i.   Accurate

ii.  Computationally efficient.

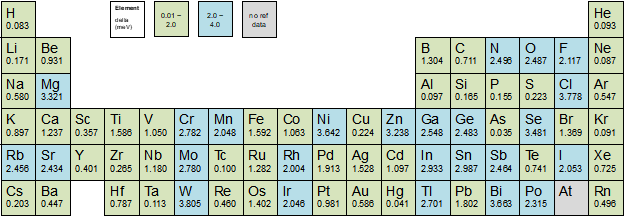
In this blog post available on LinkedIn as well, we will present a rapid overview of a few commonly used descriptions for nuclei, core electrons, and valence electrons and present our own newly optimized numerical atomic orbitals (NAO) for the Perdew-Burke-Ernzerhof (PBE) functional.

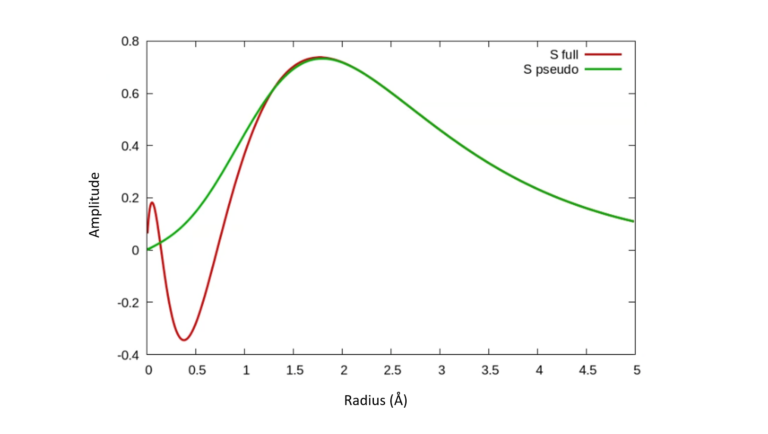
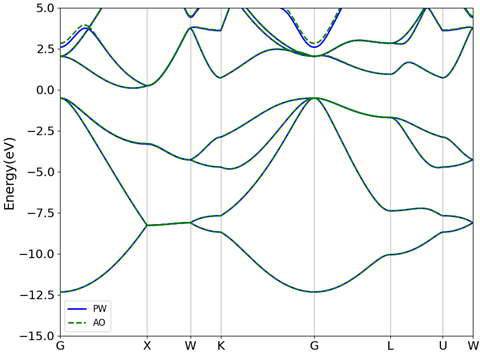
Core electrons are typically inert to the chemical environment due to their large binding energies. It is therefore possible to simplify their description by replacing the bare all-electron potential with a simpler “pseudopotential” – a term which captures the net effect of the core electrons and nucleus without the need for considering the singular Coulomb potential. The method also allows removing sharp features of valence wavefunctions near the origin. As an example, Figure 1 shows the pseudo-wavefunction of Si obtained from a pseudopotential and compares it to the wavefunction arising from the bare potential. The pseudo-wavefunction is better behaved and has less nodes and yet reproduces a charge density identical to the true wave function beyond a critical radius (~ 1 Å here).

The norm-conserving pseudopotential approach is very commonly and successfully used in the context of Density Functional Theory (DFT) calculations (Refs. 1, 2). Indeed, our orbital based DFT packages NanoDCAL and RESCU+ both adopt pseudopotential descriptions for nuclei and core electrons. In this work, we begin with the (PBE) Optimized Vanderbilt pseudopotentials from Pseudo-Dojo [Ref. 7], which are already known to agree well with all-electron results.

Valence electrons require a more complex treatment than core electrons since they are highly sensitive to the chemical environment. One commonly used approach is to adopt a plane wave (PW) decomposition for them (Ref. 3). This method is well-suited to periodic geometries like crystals and because precision is controlled by a single parameter: the energy cutoff. However, it has the drawback that it can require a very large basis set to reach sufficient accuracy. Another commonly used approach is a Numerical Atomic Orbital (NAO) expansion of the valence electrons (Ref. 4), which vastly reduces the size of the basis set. The success of this method basically depends on how well the chosen NAO basis set can indeed reproduce the PW calculations across a variety of chemical environments.

In order to optimize our NAO basis sets efficiently, we needed a quality metric which reliably indicates this transferability. Ref. 5 provides just the metric that fits our needs. This allows us to express the spread in prediction between Pseudopotential + NAO calculations to state-of-the-art PW calculations as a single number (Δ). This Δ can then be minimized to ensure that our NAO basis set is optimal. We optimize the NAO using PW data as reference rather than all-electron data to effectively decouple the pseudopotential and orbital errors and avoid overfitting.

Δ is obtained by integrating the difference between the equation of states (EOS) from PW and NAO calculations over a range of volumes (± 6% around equilibrium). Figure 2 shows a schematic from Ref. 5, where the full technical details can be found. A lower value of Δ indicates that an NAO expansion is better capable of reproducing PW results in a transferable manner across a range of chemical environments. In particular, it better predicts equilibrium volume, lattice constants and bulk modulus.

We have used RESCU to perform total energy calculations to minimize Δ for most elements in the periodic table. Figure 3 summarizes the results:

Most elements have a value of Δ < 2 meV, indicating excellent accuracy and transferability of the optimized NAO basis sets.

We provide a comparison of the PW bandstructure and a bandstructure obtained using our newly optimized NAO basis for a common semiconductor: Silicon. See Figure 4 for reference. We emphasize that the excellent agreement between the two methods does not arise from fitting any empirical parameters as is common say, in Slater-Koster methods (Ref. 6), but rather from the quality of the chosen NAO basis. This shows how optimizing Δ doesn’t only guarantee good structural properties, but transfers to the electronic structure.

We are actively exploring various optimization techniques (Stochastic, Bayesian, Nelder-Mead, etc.). In future releases, we intend to obtain higher accuracy gains for our optimized triple-zeta-polarized atomic orbitals and to also release highly optimized single-zeta-polarized and double-zeta-polarized atomic orbitals.

These brand new sets of AO are available with our atomistic tools RESCU, RESCU+, NanoDCAL and NanoDCAL+. Please check our documentation portal and our community forum for technical Q&A between our users and our team of experts.

We hope you liked it, Stay tuned for more content soon!

(1) P. Hohenberg, W. Kohn, Inhomogeneous electron gas. Phys. Rev. 136, B864–B871 (1964).

(2)  W. Kohn, L. J. Sham, Self-consistent equations including exchange and correlation effects. Phys. Rev. 140, A1133–A1138 (1965)

(3)  Ihm J, Zunger A and Cohen M L 1979 J. Phys. C: Solid State Phys. 12 4409

(4)   José M Soler, Emilio Artacho, Julian D Gale, Alberto García, Javier Junquera, Pablo Ordejón, and Daniel Sánchez-Portal. The SIESTA method for ab initio order-N materials simulation. Journal of Physics: Condensed Matter 14.11 (2002), p. 2745.

(5)  K. Lejaeghere, V. Van Speybroeck, G. Van Oost, S. Cottenier, Error estimates for solid-state density-functional theory predictions: An overview by means of the ground-state elemental

(6)  Simplified LCAO Method for the Periodic Potential Problem. Crit. Rev. Solid State 39, 1–24 (2014).

(7)  The PseudoDojo: Training and grading a 85 element optimized norm-conserving pseudopotential table. M. J. van Setten, M. Giantomassi, E. Bousquet, M. J. Verstraete, D. R. Hamann, X. Gonze, G.-M. Rignanese. Computer Physics Communications 226, 39-54 (2018).